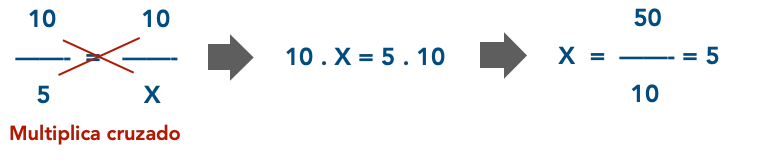Regra de três simples

A regra de três simples ocorre quando temos duas razões nas quais há 3 valores conhecidos e 1 valor desconhecido (normalmente utilizamos o x para representar o valor desconhecido).
Antes de estudarmos sobre a regra de três devemos conhecer alguns conceitos tais como: grandeza diretamente proporcional e grandeza inversamente proporcional.

Primeiramente vamos definir o que é uma grandeza. Tudo aquilo que pode ser medido, contado ou comparado chamamos de grandeza.
Exemplo: Tempo, velocidade, peso, quantidade de pessoas, volume, dentre outros. Um outro conceito que devemos saber é o de grandeza diretamente proporcional e grandeza inversamente proporcional.

Grandezas diretamente proporcionais

Duas grandezas são diretamente proporcionais quando a medida que uma grandeza aumenta a outra também aumenta na mesma proporção e a medida que uma grandeza diminui a outra também diminui na mesma proporção.

Exemplo: Tempo e distância percorrida.

Perceba que essas duas grandezas são diretamente proporcionais pois ao se aumentar uma a outra aumenta na mesma proporção.

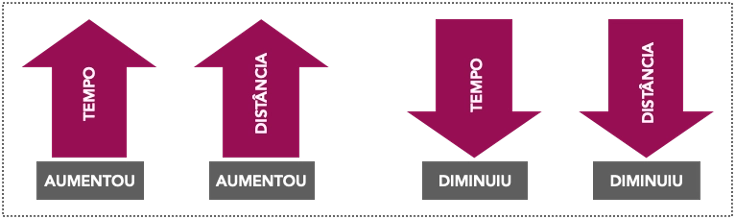
Vamos supor que você caminhando por 10 minutos, percorra uma distância de 100 metros. O que acontecerá se você, mantendo o mesmo ritmo, e aumentar a caminhada para 20 minutos? — Certamente percorrerei uma distância maior, você dirá. É isso mesmo! Você irá percorrer uma distância maior. Então quando aumentamos a primeira grandeza (tempo), aumentamos também a segunda (distância). Agora se em vez de caminhar 10 minutos, você caminha apenas 5? — Essa é fácil, a distância que percorrerei será menor. Acertou mais uma vez, você está ficando bom nisso! Então ao diminuirmos uma grandeza (tempo) a outra (distância) também diminui na mesma proporção.

O gráfico abaixo ilustra muito bem essa relação entre as grandezas tempo e distância percorrida.

Abaixo mostramos exemplos de algumas grandezas diretamente proporcionais.

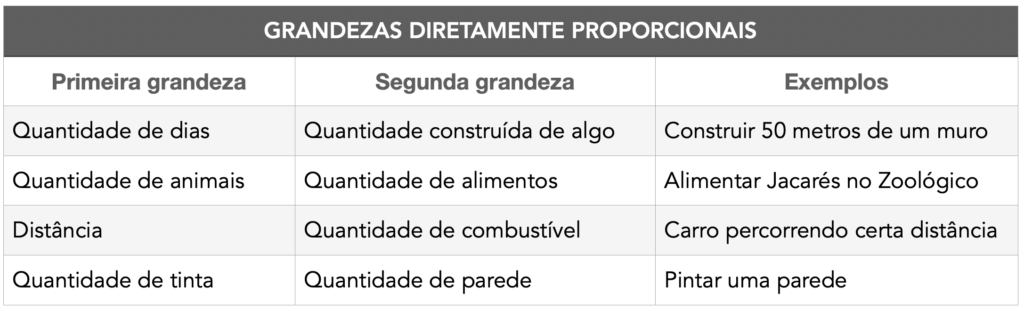
Grandezas inversamente proporcionais

Duas grandezas são inversamente proporcionais quando a medida que uma grandeza aumenta a outra diminui na mesma proporção e a medida que uma grandeza diminui a outra aumenta na mesma proporção.

Vamos analisar essas duas grandezas: velocidade média e tempo.

Essas duas grandezas são inversamente proporcionais, pois ao se aumentar uma a outra diminui. Vamos ao exemplo da caminhada. Digamos que você queira percorrer uma distância de 5 km caminhando com velocidade de 5km/h. Note que com essa velocidade o tempo para terminar essa caminhada será de 1 hora, certo? Diga-me o que acontecerá se ao invés de caminhar com velocidade de 5km/h você aumentasse os passos e conseguisse caminhar 10km/h? — Claro que chegarei em um tempo bem menor ao meu destino, você responde. Isso mesmo.

Podemos representar graficamente essas duas grandezas inversamente proporcionais, conforme abaixo.

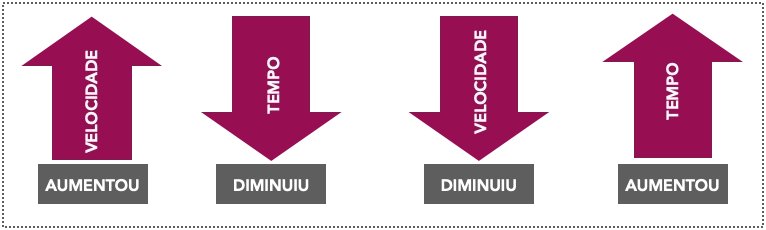
Abaixo listamos algumas grandezas inversamente proporcionais

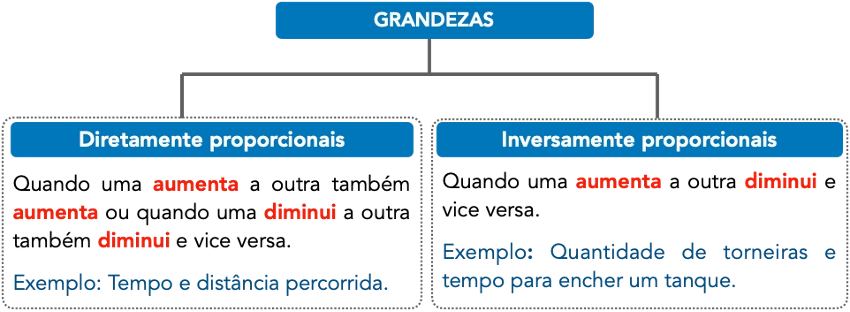
Então para resumir o conceito de grandezas proporcionais, segue o gráfico abaixo.

Regra de três simples

A regra de três simples ocorre quando há duas grandezas as quais possuem três valores conhecidos e um valor desconhecido. Nesse caso teremos dois valores para a primeira grandeza e dois valores para a segunda grandeza (uma conhecida e outra desconhecida). A regra de três simples possui apenas duas colunas.

Veja como esquematizar a regra de três.

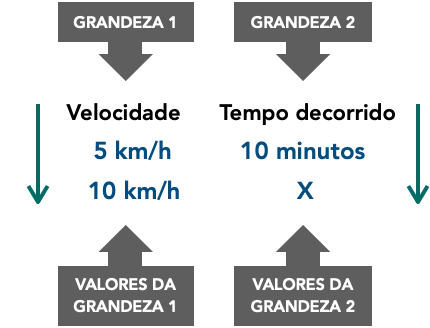
Agora vamos esquematizar uma passo a passo para resolução de problemas de regra de três simples.

• Passo 1: Extrair os dados do comando da questão e colocá-los em duas colunas (duas grandezas). Lembre-se que a coluna deve ter valores de mesmo tipo. Por exemplo: Se tivermos duas colunas (velocidade e tempo). A coluna velocidade deve ter apenas valores de velocidade e a coluna tempo deve ter apenas valores de tempo.

• Passo 2: O valor desconhecido (normalmente x) ficará em uma das colunas de acordo com o enunciado da questão. O valor desconhecido é o que deve ser calculado.
• Passo 3: Quando tiver colocado as informações nas duas colunas, basta colocar uma seta (para baixo ou para cima) apontando para o valor desconhecido de x na coluna em que ele estiver.

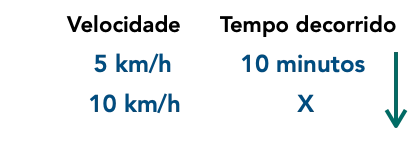
• Passo 4: Fazer a análise das grandezas para saber se são diretamente ou inversamente proporcionais. Esse é um dos passos mais importantes. Nesse momento você irá comparar as duas colunas perguntando o seguinte: se a coluna da velocidade aumentar, a coluna do tempo decorrido aumentará? Se a resposta for sim, estamos diante de uma grandeza diretamente proporcional. Caso contrário a grandeza será inversamente proporcional.
  
  Há outra forma de analisar: se a velocidade diminuir o tempo decorrido diminuirá? Se sim estamos diante de grandezas diretamente proporcionais. Caso contrário as grandezas serão inversamente proporcionais.
  
• Passo 5: Após isso coloque uma seta na coluna que não há o valor de x da seguinte forma: se as grandezas forem diretamente proporcionais a seta irá ficar na mesma direção ao da coluna em que há o x. Se as grandezas forem inversamente proporcionais a seta irá ficar na direção oposta ao da coluna em que há o valor de x.
  

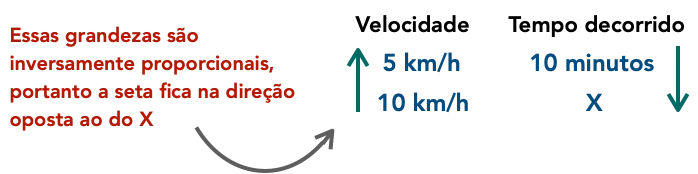
• Passo 6: Seguindo adiante, vamos fazer o alinhamento das setas. Se as setas estiverem apontando para a mesma direção basta apenas montar a regra de três na forma que está. Dessa forma:
  

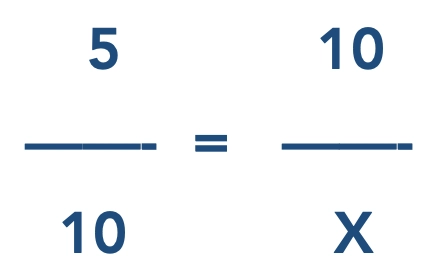
• Passo 7: Por outro lado se as setas estiverem apontando para direções opostas, inverter os valores da coluna em que não há o valor de x e depois montar a regra de três. Por exemplo:

• Passo 8: Por fim basta efetuar os cálculos.