Razão e Proporção

Razão

Razão é a divisão ou quociente entre dois números (grandezas). Tem como objetivo relacionar duas grandezas. Representamos simbolicamente assim:

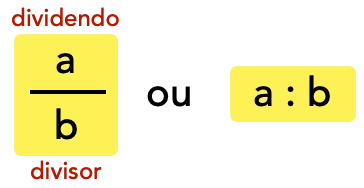
Algumas expressões que representam uma razão:

Exemplo:
Em uma sala de aula há 45 mulheres e 30 homens. Qual a razão entre o número de homens e o número de mulheres.

Como a razão é entre homens e mulheres podemos representar assim: 30/45. Simplificando fica 30/45 = 2/3. Isso significa que para cada 2 homens, temos 3 mulheres.

Proporção

A proporção é a igualdade entre duas razões, ou seja, se duas razões são iguais dizemos que elas são proporcionais.

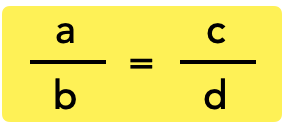
Algumas formas que representam uma proporção:

Propriedades da proporção

Primeira propriedade

Seja a relação:  a/b = c/d   

A seguinte propriedade é verdadeira: b x c = a x d. Os números a e d são chamados de extremos, já os números b e d são chamados de meios. Por isso acredito que em algum dia da sua vida você ouviu seu professor afirmar que “O produto dos meios é igual ao produto dos extremos”. E o que isso quer dizer? Simples. A multiplicação cruzada gera uma igualdade algébrica.

Exemplo: 2/3 = 4/6

Quais são os números que representam os meios? — você responde, 3 e 4. E quais os números que representam os extremos? — Fácil professor, são o 2 e o 6, — você responde confiante.

Agora faça o produto (significa multiplicação) dos meios 3 e 4. Teremos como resultado o valor de 12, pois 3 x 4 é igual a 12.

Nesse momento faça o produto dos extremos 2 e 6. O resultado certamente é 12, pois 2 x 6 é igual a 12.

Se sua mente, nesse momento, não estiver em marte, certamente percebeu que os resultados são iguais, ou seja, o produto dos meios é igual ao dos extremos. Fácil, né?

Segunda propriedade

Seja a relação a/b = c/d = (a + b)/(b + d).

Quaisquer das duas primeiras frações é igual a soma dos numeradores dividido pela soma dos denominadores. Dito isso, a seguinte relação é verdadeira:

Grandezas diretamente proporcionais

Em uma fábrica há uma máquina que produz parafusos de acordo com a tabela abaixo.

De acordo com a tabela, a máquina operando por 6 minutos, produz 2 parafusos. Com 9 minutos de operação, produz 3 parafusos e com 12 minutos de operação, produz 4 parafusos.

Grandezas diretamente proporcionais ocorrem quando a razão entre elas são sempre iguais.

Vimos pela tabela que quando a máquina opera por 6 minutos, produz 2 parafusos. Assim temos uma razão de 6/2. Igualmente quando a máquina leva 9 minutos para produzir 3 parafusos, dizemos que a razão é 9/3. Por fim quando a máquina leva 12 minutos para produzir 4 parafusos, a razão é 12/4.

As razões 6/2, 9/3 e 12/4 são iguais, visto que se dividirmos o numerador pelo denominador de cada uma das frações obteremos o mesmo valor para as três frações. No caso em questão o resultado é 3. Esse valor é chamado de constante de proporcionalidade (ou coeficiente de proporcionalidade) e normalmente utilizamos a letra “k” para representá-la. No nosso exemplo o valor de k = 3.

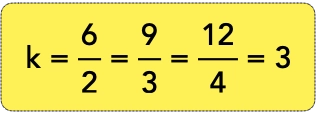
Podemos concluir que os números 6, 9 e 12 são diretamente proporcionais aos números 2, 3 e 4.

Nesse momento a única coisa que você deve lembrar é que para grandezas diretamente proporcionais o valor de k se obtém dividindo o numerador pelo denominador.

Nota 1: Note que nas grandezas diretamente proporcionais a medida que os numeradores aumentam, os denominadores aumentam na mesma proporção.

Nota 2: O valor de k indica quantas vezes o numerador é maior ou menor que o denominador. O numerador será maior quando o valor de k for maior que 1 e será menor quando o valor de k estiver entre 0 e 1.

Grandezas inversamente proporcionais

Uma determinada precisa de um serviço de pintura em sua casa. Porém antes de contratar os pintores realizou alguns orçamentos conforme tabela abaixo: 

Se essa pessoa contratasse 2 pintores, levaria 20 dias para concluir o serviço de pintura. Contratando 4, levaria 10 dias. E contratando 8 pintores, levaria 5 dias para realizarem a pintura. De acordo com a tabela temos as razões: 2/20, 4/10 e 8/5. Perceba agora que, quando  dividimos o numerador pelo denominador teremos valores diferentes. Entretanto se multiplicarmoso numerador pelo denominador, teremos valores iguais, que nesse caso é 40, pois 2 x 20 = 4 x 10 = 8 x 5. Por isso em grandezas inversamente proporcionais a constante de proporcionalidade “k” é obtida pela multiplicação entre o numerador e o denominador.

Nunca esqueça que nas grandezas inversamente proporcionais a constante “k” é obtida multiplicando o numerador pelo denominador. Já nas grandezas diretamente proporcionais a constante “k” é obtida dividindo o numerador pelo denominador.

Mais um detalhe. Veja na tabela que a medida que o numerador aumenta, o denominador diminui na mesma proporção. Isso indica que são grandezas inversamente proporcionais.

— Professor fiquei com dúvida. Compreendi as grandezas inversamente proporcionais, mas não consigo ver onde está “o inversamente” nessas grandezas, visto que só multiplicamos — você indaga.

Vou te contar um segredo, mas não conta para ninguém. Nós utilizamos a multiplicação com a finalidade de facilitar o entendimento e os cálculos.  Quando dizemos que os números 2, 4 e 8 são inversamente proporcionais aos números 20, 10 e 5, na verdade queremos dizer que os números 2, 4 e 8 são diretamente proporcionais ao inversos de 20, 10 e 5. Veja isso:

Viu como são iguais? — Tudo bem, mas não entendi a parte do inverso de um número. — você diz.

Para realizar o inverso de um número basta inverter o numerador com o denominador. Em números que não estão em forma de fração o inverso se dá divido 1 pelo respectivo número. Por exemplo, o inverso de 20 é 1/20 ,ou seja, pego o 1 e divido por 20, só isso.

Para maior aprofundamento leia a aula sobre divisão e multiplicação de frações.

Divisão de um número em partes diretamente proporcionais

Para resolvermos questões sobre divisão em partes proporcionais devemos saber que a seguinte propriedade é válida para as proporções:

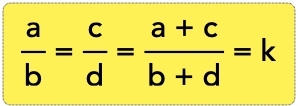
Essa propriedade nos mostra que quando temos razões proporcionais podemos somar os numeradores e dividir pela soma dos  denominadores que formaremos assim outra proporção equivalente às primeiras. Dessa forma se a divisão é em partes diretamente proporcionais, para encontrar o valor de k, basta pegar o total e dividir pela soma das partes proporcionais.

Exemplo: Dividir 12 em partes proporcionais a 2 e 4.

Total = 12 (valor de A + C) B = 2              D = 4

Aplicando a fórmula A/B = C/D = (A + C)/(B + D), temos:

A/2  = C/4 = 12/(2+4) = k

Para saber o valor de k, pegamos a última fração. Assim k = 12/(2+4) = 12/6, — k = 2.

Calculamos a primeira fração: A/2 = k, ou seja, A = 2.k  A = 2.2  A = 4

Calculamos a segunda fração C/4 = k, ou seja, C = 4.k  C = 4.2  C = 8.

Portanto as partes proporcionais são 4 e 8 respectivamente. Isso quer dizer que ao dividir 12 em partes diretamente proporcionais a 2 e 4, essas partes serão 4 e 8, pois  (4 + 8) =12.

Poderíamos ter realizado o seguinte esquema:

Vamos considerar que A+B=12. Assim, temos: A/2 = B/4 = (A+B)/(2+4)  A/2 = B/4 = 12/6

Portanto, A/2 = 12/6  6A=12.2  A= 24/6  A = 4

B/4 = 12/6    6.B = 12.4    B = 48/6   B = 8

Em resumo para dividir um número em partes diretamente faço assim:

Calculo o valor de k, pegando o total e dividindo pela soma dos denominadores das frações.

Depois igualo cada fração ao valor de k, calculando o valor dos numeradores A e B.  Esses serão o resultado da divisão diretamente proporcional do total em questão.

Divisão de um número em partes inversamente proporcionais

— Mas quando a divisão é realizada em partes inversamente proporcionais? — você questiona. Excelente pergunta. Vou mostrar dois processos.

Primeiro processo:

Usando a seguinte propriedade das proporções.

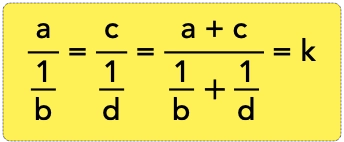
— Ué! acho que já vi isso em algum lugar. — você deve estar pensando. Realmente já vimos isso quando tratamos de grandezas inversamente proporcionais. A propriedade acima se parece com a divisão em partes diretamente proporcionais. Na verdade, é a mesma. Acontece que nessa os denominadores são os inversos (o inverso acontece quando o numerador vai para baixo e o denominador vai para cima, ou seja, há uma troca entre a parte de baixo e a parte de cima).  

Exemplo: Dividir 1350 em partes inversamente proporcionais a 3, 6 e 8.

Vamos aplicar a fórmula:

Calculamos o valor de k:

A/(1/3)  = B/(1/6) = C/(1/8) = (A+B+C)/(1/3 + 1/6 + 1/8) = k    k = 1350/(1/3 + 1/6 + 1/8) = 1350/(15/24)   k = 2160

Igualamos cada fração ao valor de k para encontrarmos os valores de A, B e C.

A/(1/3) = k    A/(1/3) = 2160   A = 2160 x 1/3    A = 720

B/(1/6) = k    B/(1/6) = 2160   B = 2160 x 1/6    B = 360

C/(1/8) = k    C/(1/8) = 2160   C = 2160 x 1/8    C = 270

Tudo que fizemos acima já vimos anteriormente, não é nenhum segredo para você isso.

O segundo processo funciona assim: iremos utilizar o mesmo procedimento da divisão em partes diretamente proporcionais. Bem, não é o mesmíssimo procedimento.

O segundo processo funciona assim: iremos utilizar o mesmo procedimento da divisão em partes diretamente proporcionais. Bem, não é o mesmíssimo procedimento. Iremos mudar um pequeno detalhe. A única coisa que iremos mudar é transformar as partes inversamente proporcionais em partes diretamente proporcionais. — Mas como é isso? — você questiona. É relativamente simples. Vamos tirar o mmc das partes inversamente proporcionais e depois dividir o mmc por cada uma dessas partes. O resultado dessa divisão serão partes diretamente proporcionais. Daí podemos aplicar  o mesmo procedimento da divisão em partes diretamente proporcionais.

Exemplo: Dividir 1350 em partes inversamente proporcionais a 3, 6 e 8.

As partes inversamente proporcionais são 3, 6 e 8. Vamos transformar essas partes inversamente proporcionais em diretamente proporcionais.

Primeiro passo: Tirar o mmc entre 3, 6 e 8. Então o mmc (3, 6, 8) = 24

Segundo passo: dividir o mmc por cada parte inversamente proporcional. 24/3 = 8, 24/6 = 4, 24/8 = 3. Assim, transformamos as partes inversamente proporcionais (3, 6 e 8) em partes diretamente proporcionais (8, 4 e 3) respectivamente.

Terceiro passo: aplicar a regra da divisão em partes diretamente proporcionais.

Valor de A/8 = B/4 = C/3 = (A+B+C)/(8+4+3)  = 1350 /(8+4+3) = 1350/15  k = 90

A/8 = k     A = 8.k  A = 8.90  A = 720

B/4 = k     B = 4.k  B = 4.90  B = 360

C/3 = k     C = 3.k  C = 3.90  C = 270

Divisão de um número em partes diretamente e inversamente proporcionais ao mesmo tempo.

Todos os procedimentos anteriormente realizados servirão para solucionar esse tipo de divisão. Veja abaixo a fórmula que utilizamos para fazer esse tipo de cálculo.

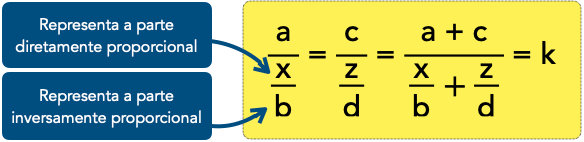
Os numeradores x e z representam a partes diretamente proporcionais. Já os denominadores b e d representam as partes inversamente proporcionais. Pronto. Basta aplicar a resolução que já estudamos por aqui.

Bons estudos e até a próxima!

━◦○◦━◦○◦━