Equação do primeiro grau
Nessa aula iremos abordar os seguintes assuntos:
O que é uma equação?
Equação é uma igualdade que possui um ou mais valores desconhecidos, também chamados de incógnitas.
Vamos analisar as duas palavras mais importantes dessa definição. A primeira: igualdade. A segunda: incógnitas.
Igualdade
Quando falamos em equação, a igualdade pode ser comparada a uma balança que está equilibrada. Quando, por exemplo, existir duas maçãs em cada lado da balança percebemos que ela está equilibrada (supondo que as maças são idênticas). Entretanto ao retirarmos uma maça do lado esquerdo, perceberemos que a balança ficará desequilibrada, pendendo para baixo no lado direito. Agora se quisermos novamente equilibrar essa balança poderíamos retirar uma maça do lado direito e ambos os lados ficariam com apenas uma maça, voltando ao equilíbrio inicial.

Nesse momento você deve estar pensando: entendi como funciona e igualdade da balança com maças, mas quero saber como funciona com números. Alias eu nem gosto de maças. Como agora sei que não gosta de maças, sugiro que troque as maças por números. O funcionamento do equilíbrio da balança utilizando maças segue o mesmo princípio da equilíbrio com os números. Imagine nesse instante que no lado direito da balança tenha o número dois e do lado esquerdo também tenha o número dois. Você há de concordar que a balança está em equilíbrio, né? Entretanto se por acaso houver no lado esquerdo da balança o número três e do lado direito o número quatro, a balança não estará equilibrada, o equilíbrio foi ao infinito e além.
Vamos usar a imaginação nesse momento. Crie em sua mente uma balança em que nos dois lados tenha o número quatro. A balança estará em equilíbrio. Uma pergunta importante: como podemos sempre manter essa balança imaginária em equilíbrio? Ao responder essa pergunta você estará apto a operar com qualquer equação que apareça em sua frente. Então para sempre mantermos a balança equilibrada, basta sempre manter ambos os lados com os mesmos números de elementos. Veja que em nossa balança temos quatro de ambos os lados. Se somarmos um ao lado direito, devemos também somarmos um ao lado esquerdo, cujo resultado ficará cinco em ambos os lados. Se subtrairmos um ao lado esquerdo devemos também subtrair um ao lado direito, cujo resultado ficará três. Agora vou lhe mostrar a regra de ouro de como sempre manter a balança equilibrada: basta somar, subtrair, dividir ou multiplicar o mesmo número de ambos os lados. Pronto!

Mas como aplico isso na equação? Simples. O lado esquerdo da balança é primeiro membro da equação, o lado direito é o segundo membro da equação. Já o equilíbrio da balança é a igualdade. Lembre-se, em uma equação sempre mantenha a igualdade em equilíbrio. Agora você é um expert em equação.
Incógnita
A incógnita é um valor desconhecido de forma que sua descoberta é a solução de uma equação. Normalmente utilizamos a letra x para representar uma incógnita, porém nada impede de se utilizar outras letras do alfabeto, ou até mesmo símbolos. A letra em si não carrega significado algum. O mais importante é saber que ela representa um valor que queremos descobrir.
Pois bem, acho que você está questionando como surgiu a ideia de trocar um número de sinal ao deslocar esse número de um lado para o outro da igualdade. Na verdade essa técnica é um método prático de sempre manter a igualdade verdadeira, ou seja, manter nossa balança sempre equilibrada.
Vejamos a seguinte igualdade 2 = 2. Agora iremos subtrair uma unidade em ambos os lados da igualdade. Fica assim: 2 – 1 = 2 – 1. O resultado dessa igualdade será 1 = 1. Veja que antes a igualdade era verdadeira ( 2 = 2) e agora subtraindo uma unidade de ambos os lados da igualdade ainda permanece verdadeira (1 = 1). Veja que quando 1 = 1, podemos reescrever a igualdade assim: 1 – 1 = 0, certo? Para cancelar esse -1 devo somar +1 em ambos os lados. A nova configuração será: 1 – 1 +1 = 0 + 1. Então para cancelar um número devemos fazer a operação oposta a esse número. O número é positivo, subtraio. É negativo, somo. Estou diante de uma divisão, multiplico. É uma multiplicação, divido. Assim quando trocamos o número de um lado para outro trocando de sinal estamos apenas cancelando esse número e mantendo a igualdade verdadeira. Estamos tornando esse número neutro.
Na equação 2 = 2, se movermos o 2 para o lado direito, trocando de sinal manteremos a igualdade verdadeira. Estaremos cancelando esse número e assim mantendo a igualdade verdadeira. Fica assim: 0 = 2 – 2, ou seja, 0 = 0. Recapitulando, quando mudo o número de um membro para outro, trocando de sinal, estou cancelando esse número e por consequência, mantendo a igualdade verdadeira.
Equação do primeiro grau
Até falamos sobre a equação. Mas o que significa uma equação de primeiro grau? É isso que nos propomos a responder. Uma equação de primeiro grau é a equação na forma ax + b = 0, em que a e b são números reais e a é diferente de 0. A forma de reconhecer uma equação de primeiro grau é observarmos o expoente da incógnita x. Se o maior expoente da equação igual a 1, então a equação é de primeiro grau (quando for 1, não há necessidade de escrevê-lo. por isso o expoente 1 não aparece junto ao x).
Como exemplo traremos a equação 2x – 4 = 0. Vamos conhecer algumas partes da equação. O valor de a é igual a 2 (a que está próximo ao x). O valor desconhecido é o x. Já o valor de b é igual a 4.
A raiz de uma equação do primeiro grau
A raiz de uma equação é o valor que x deve assumir para que a equação seja verdadeira. Na equação 2x – 4 = 0, o único valor de x que faz com que ela seja verdadeira é quando x assume o valor 2, pois 2.2 – 4 = 0, assim 4 – 4 = 0. Por isso a raiz da equação 2x – 4 = 0 é igual a 2.
Soluções de uma equação do primeiro grau.
Uma equação pode assumir as seguintes quantidades de soluções:
- Uma única solução.
- Infinitas soluções
- Nenhuma solução.
Única solução
Um exemplo de equação que possui apenas uma única solução é a equação 2x = 4. Nela existe apenas um valor de x que torna a equação verdadeira, ou seja, a equação possui apenas uma única raiz. Dessa forma só existe um valor de x que multiplicado por 2 dê igual a 4. Assim a raiz dessa equação é 2, pois 2.2 = 4, 4 = 4.
Infinitas soluções
Como exemplo de equação com infinitas soluções temos: 0x = 0. Veja que qualquer valor que se atribua a x, sempre teremos uma igualdade verdadeira, pois qualquer número multiplicado por zero sempre teremos como resultado zero. Assim 0.1 = 0, que resulta 0 = 0, ou 0.2 = 0, que resulta 0 = 0. Não importa se o valor de x for 0 ou um milhão que a equação sempre será verdadeira. Pegou a visão?
Nenhuma solução
A equação 0x = 4 não possui nenhuma solução. Tente encontrar um número que multiplicado por zero tenha como resultado 4. Já adianto que você não irá encontrar esse número, por mais que você tente, visto que não há nenhum número que multiplicado por zero, dê igual a 4. Então essa equação nunca será verdadeira, não possui raiz real.
O gráfico da equação do primeiro grau
Antes de tudo vamos falar sobre o plano cartesiano. Nele podemos determinar pontos em um plano. O sistema cartesiano possui dois eixos: o primeiro: o horizontal, chamado de abscissa. O outro: o vertical, chamado de ordenada. O eixo das abcissas é representado pela letra x, já o eixo da ordenada é representado pela letra y. Como faço para aprender tudo isso? É muita informação para uma cabecinha só, você deve estar pensando. Não se preocupe. Há uma forma de não esquecermos os nomes dos eixos x e y. Vamos lembrar da seguinte maneira: Qual a letra mais lembrada quando se fala em equação? O x, você responde! Acertou! Qual a primeira letra do alfabeto? Letra a, você grita! Amarre as duas informações e saberá que a abscissa está ligada ao eixo x pelo grau de importância que a letra a e a letra x possuem. Uma outra forma de memorizar é chamar a abscissa de abscixa (com x mesmo, só não diga para teu professor de português que eu lhe ensinei isso).
Marcando os pontos no gráfico cartesiano.
Vamos ao passo a passo par realizar as marcações dos pontos no gráfico cartesiano.
Em primeiro lugar trace uma reta horizontal e faça marcações nela que tenham uma mesma distância.
Agora trace uma reta vertical cruzando com a linha horizontal anteriormente criada de forma a desenha uma cruz. Faça marcações nela também do mesmo modo como na horizontal. No centro da cruz está localizado o ponto central do plano cartesiano, a localização 0,0.

Vamos alocar os números no plano cartesiano da seguinte forma: no eixo x, tendo como referência o ponto central, movimentando-se para a esquerda, temos os valores negativos. Movimentando-se para a direta, temos os valores positivos. No eixo y, tendo como referência o ponto central, movimentando-se para baixo temos os valores negativos. Movimentando-se para cima temos os valores positivos.
No eixo x os números crescem a medida que nos deslocamos para a direita e decrescem a medida que nos deslocamos para a esquerda. No eixo y os números crescem a medida que nos deslocamos para cima e decrescem a medida que nos deslocamos para baixo.
O plano cartesiano possui quatro regiões: primeiro quadrante, segundo quadrante, terceiro quadrante e quarto quadrante.
Como desenhar a equação de primeiro grau no gráfico cartesiano
Como exemplo utilizaremos a equação y = 2x – 4.
Quando x = 1, temos y = 2.1 – 4, 2 – 4 = -2, portanto x=1 e y = -2
Quando x =3, temos y = 2.3 – 4, 6 -4 = 2, portanto x=3 e y= 2
De posse dessas coordenas, iremos traça-las no plano cartesiano.
O primeiro ponto (x, y) = (1,-2). No eixo de x contamos uma unidade para a direita a partir do ponto central. No eixo de y contamos duas unidade para baixo a partir do ponto central. Traçando uma linha paralela aos eixo teremos o cruzamento delas. Essa é a primeira coordenada.
O segundo ponto (x,y) = (3,2). No eixo de x contamos três unidades para a direita a partir do ponto central. Já no eixo de y, contamos duas unidades para cima a partir do ponto central. Traçando um linha paralela aos eixos teremos o cruzando delas. Obtemos assim segunda coordenada.
Basta agora ligarmos os dois pontos por meio de uma reta. Esse reta que traçamos é o gráfico da equação do primeiro grau.
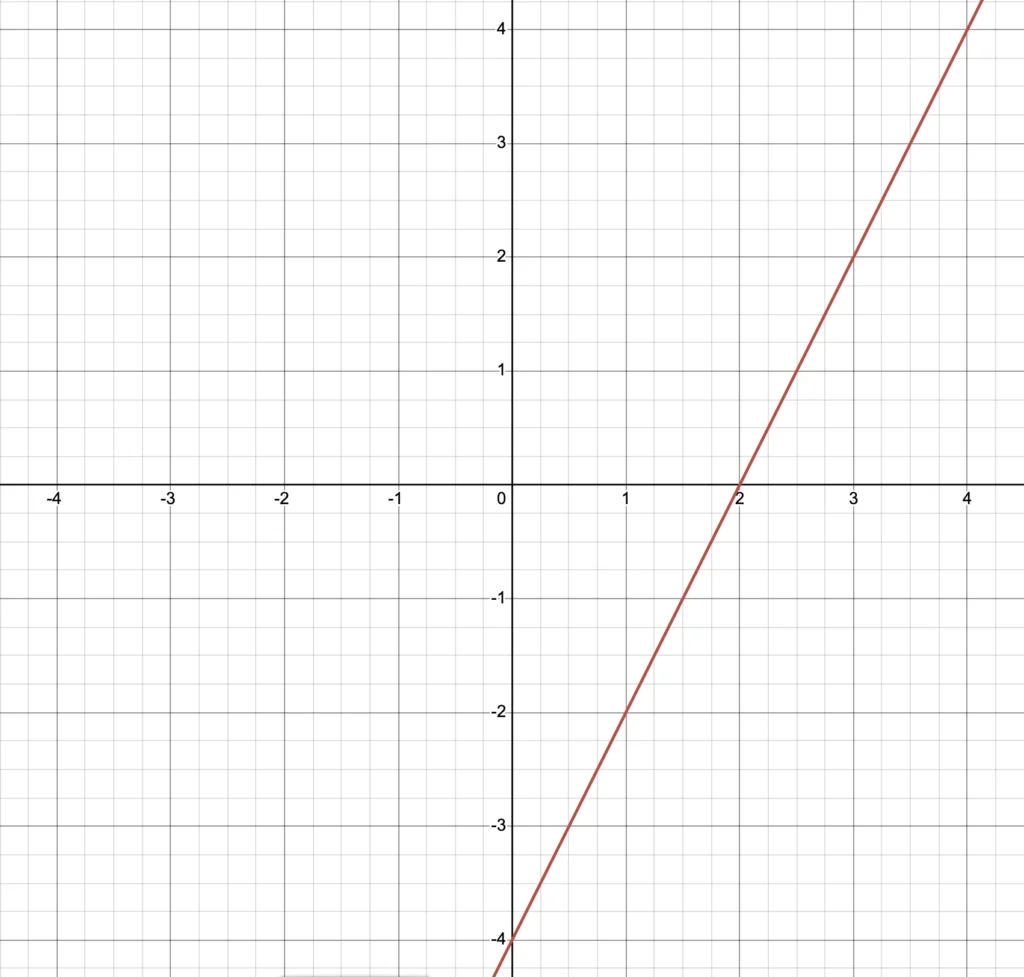
Há outros detalhes importantes a considerar sobre a equação y = 2x – 4:
Como já vimos anteriormente a =2 e b=-4. Perceba que o gráfico corta o eixo de y quando y=-4
A raiz da equação está localizado onde a reta corta o eixo x, nesse caso no 2.
Bem, acho que você já entendeu como funciona a equação de primeiro grau.
O que eu deseja agora é: tenha bons estudos.