Como calcular a porcentagem

É muito simples entender a porcentagem. Ela é nada mais do que dividir por 100. Só isso. Quando dizemos que algo é 10%, quer dizer que devemos pegar esses 10 e dividi-lo por 100. Nesse caso o resultado é 0,10. A partir de então pegamos 0,10 e multiplicamos pelo valor que queremos aplicar os 10%.

O símbolo para representar a porcentagem é % (acho que todos já conhecem, isso faz parte de nosso dia a dia).

A porcentagem pode ser representada das seguintes formas:

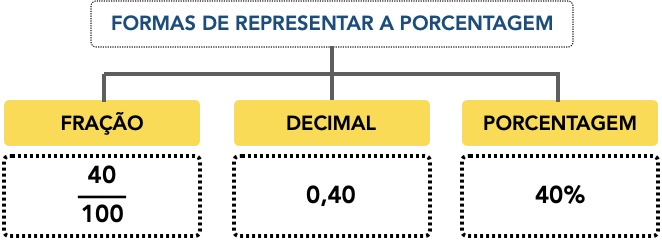
No exemplo acima todas essas formas são iguais, ou seja, possuem os mesmos valores. Na resolução de questões use a forma mais conveniente para facilitar os cálculo de porcentagem.

Como transformar a taxa percentual em taxa unitária (ou decimal)

Uma forma prática de realizar essa conta é deslocar duas casas decimais:

• de taxa percentual para taxa decimal  desloca  a vírgula duas casas para a esquerda.
• de taxa decimal para taxa percentual  desloca  a vírgula duas casas para a direita.

Segue abaixo o diagrama de como converter a taxa percentual para taxa decimal de e vice-versa.

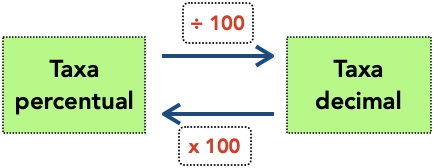
Vamos exemplificar como realizar a conversão das taxas descrita anteriormente.

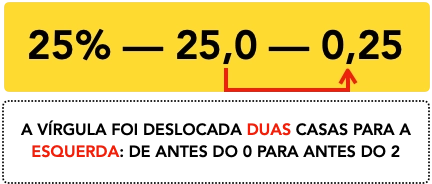
Exemplo 1: transformar  25% em taxa decimal

25% é o mesmo que 25 dividido por 100, então pego o 25 e divido por 100, cujo resultado é 0,25 (basta deslocar duas casas decimais para a esquerda). Veja o esquema abaixo:

Exemplo 2: transformar 0,25 em taxa percentual

0,25 é o mesmo que 25 dividido por 100. Pegue agora o 25 e desloque duas casas decimais para a direita para se obter o valor em porcentagem. Nesse caso o valor é 25%. O esquema abaixo mostra como isso é realizado.

 Dica importante: para se calcular 10% de um número, basta   deslocar a vírgula  uma casa para a esquerda desse número. Agora para se calcular 1%, basta deslocar duas casas para a esquerda.

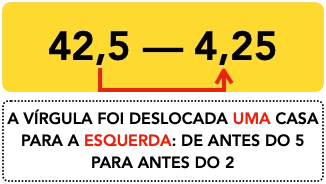
Exemplo 1: Calcular 10% de 42,5.

Como quero calcular 10% de 42,5, pego o número em questão e desloco um casa decimal para a esquerda. Então o 42,5 se transforma em 4,25. Isso significa que 10% de 42,5 equivale a 4,25. Fácil, né? Veja como fica o esquema abaixo.

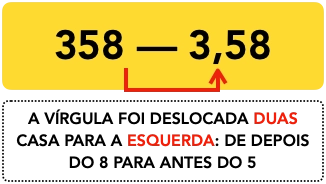
Exemplo 2: Calcular 1% de 358

Pra calcular 1% de um número, devemos pegar esse número e dividi-lo por 100. Isso quer dizer que se eu quero calcular 1% de 358, devo dividir esse número por 100 cujo resultado é 3,58 (lembre-se que dividir algum número por 100, deve-se deslocar duas casas decimais para a esquerda). Esquematizando, temos:

Como entender o cálculo de porcentagem

Para se calcular x porcento de algum número, significa que eu devo pegar esse número e multiplicar pela porcentagem (em valores decimais). É importante que você saiba de cor que 100% de algo é a sua totalidade, 50% de algo é sua metade. Outro detalhe é que a palavra “de” significa “multiplicação”

A partir disso vamos analisar três situações possíveis:

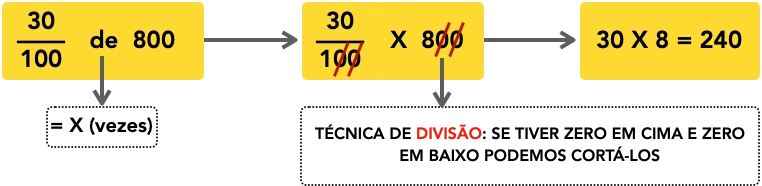
a) Como calcular 30% de 800

Iremos utilizar a forma de taxa decimal a fim de facilitar os cálculos.

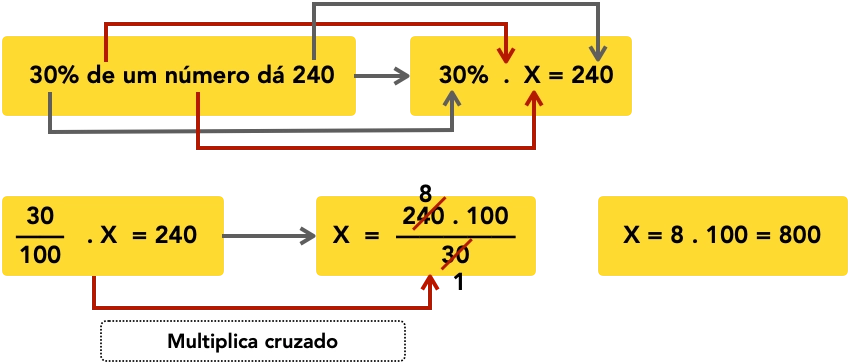
b) 30% de um número dá 240. Que número é esse?

Esse problema devemos obter um número tal que multiplicado por 30% tenha como resultado 240. Assim podemos traduzir esse enunciado da seguinte forma: 30% de X = 240.

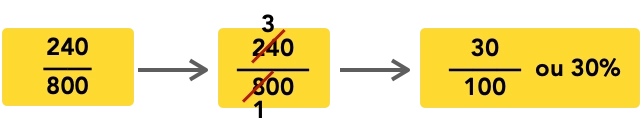
c) 240 corresponde a quantos porcento de 800

Esse cálculo indica quão próximo o 240 está de 800. Explico. Vamos pegar outro número, por exemplo, 400. Sabemos que 400 é a metade de 800, por isso, 400 é 50% de 800. 200 corresponde a 1/4 (25%) de 800. Ora, com isso sabemos que 240 corresponderá a a um valor que está entre 25% e 50%. de 800.

Há um método para se calcular quantos porcento, um valor cabe em outro. Basta dividirmos o número pelo valor de referência. No exemplo anterior devemos pegar o 240 e dividir por 800. Então 240/800

Aumento de x porcento de um valor

Método comum

Se quero aumentar em x porcento de um determinado valor, devo pegar esse valor e multiplicar pela porcentagem e logo após somar o resultado dessa multiplicação ao valor inicial. Pronto!

Vamos ao exemplo: aplicar um aumento de 30% sobre 400.

Primeiro passo: multiplico a porcentagem ao valor. 30% x 400 = 0,3 x 400 = 120

Segundo passo: somo o resultado da multiplicação pelo valor inicial. 120 + 400 = 520. Simples, né?

Porém esse não é o método mais eficiente para realizar esse tipo de cálculo. A partir de agora vou mostrar um método mais eficiente de calcular um aumento percentual. Vamos utilizar o mesmo exemplo anterior.

Método avançado

Aplicar um aumento de 30% sobre 400.

Sabemos que o valor completo, cheio corresponde a 100%, então o valor de 400 corresponde a 100% do valor, correto? Se queremos um aumento de 30% devemos somar 30% + 100% = 130%. Já temos conhecimento suficiente nesse momento para sabermos que 130% é igual a 1,30. Agora que vem o pulo do gato. Toda vez que quisermos aplicar uma aumento de 30% sobre determinado valor, basta multiplicar esse valor por 1,3. Pronto, é só isso. — Sério? — você deve estar pensando. Sim, estou falando sério.

Então vamos calcular o aumento de 30% sobre 400. Fica 400 x 1,3 = 520. Como eu disse, é muito simples. Agora vou te contar um segredo. Esse método serve para qualquer aumento percentual. — E como faço isso? — você diz.

Pegue a porcentagem inicial e some com 100%, depois multiplique esse resultado com o valor que queira aplicar o aumento. Mais um exemplo para não ficar dúvidas.

Aplicar um aumento de 50% sobre 200.

Some a porcentagem inicial 50% mais 100%, ficando 50% + 100% = 150% (lebre-se de transformar para o formato decimal). 150% = 1,5. Agora vamos multiplicar pelo valor que queremos aumentar. 200 x 1,5 = 300. Entendeu? ou quer que desenhe, brincadeirinha!

Desconto de x porcento de um valor

Método comum

Vamos ao método comum, sim, aquele que todos fazem. Primeiro multiplico o valor que quero aplicar o desconto pelo percentual de desconto. O resultado dessa multiplicação subtraio do valor inicial.

Exemplo: Aplicar um desconto de 10% sobre 150.

Lembrando que 10% é o mesmo que 0,1. Vamos multiplicar a porcentagem pelo valor que queremos aplicar o desconto, ou seja, 150 x 0,1 = 15. Esse resultado iremos subtrair do valor inicial. Ficará 150 – 15 = 135. Então quando aplico um desconto de 10% sobre 150 tenho como resultado 135.

Método avançado

Quando aplicamos o método avançado para calcular o aumento de um valor , pegamos a porcentagem e somamos com 100%. Lembra disso? Mas nesse caso não queremos um aumento, queremos um desconto. — Então professor, quer dizer que nesse caso devo subtrair o valor da porcentagem de 100%? — você perguntou. Acertou!! É isso mesmo. No método avançado vamos subtrair o percentual de desconto ao 100%, depois multiplicamos o resultado pelo valor que queremos aplicar o desconto.

Vamos calcular um desconto de 30% sobre 400

Primeiro vamos pagar os 100% e subtrair 30%. Então 100% – 30% = 70%. Lembre-se que 70% = 0,7. Depois multiplicamos pelo valor que queremos aplicar o desconto, ou seja, 400 x 0,7 = 280. Então quando aplico um desconto de 30% sobre 400 tenho como resultado o valor de 280.

— Você deve estar pensado — é sério, isso. Não acredito que dê certo.

Já que você está cético, vamos aplicar o desconto utilizando o método comum ao exemplo anterior.

Multiplicando o percentual ao valor que queremos aplicar o desconto, assim 400 x 30%, ou 400 x 0,3 = 120. Agora vou subtrair 120 de 400, ou seja, 400 – 120 = 280. Acho que agora converti você ao método avançado.

Você pode calcular o desconto ou aumento por qualquer dos métodos, mas acredito que o método avançado ganha em eficiência por fazer menos cálculos. Veja que poderíamos fazer as contas de cabeça nos exemplos acima pelo método avançado.

Aumentos e descontos sucessivos

Aumentos sucessivos

Nos aumentos sucessivos você nunca ganha. Aprenda essa frase e nunca mais esqueça o princípio sobre aumentos sucessivos. Vamos supor hipoteticamente que você esteja devendo 300 reais a alguém. Você propôs pagar essa pessoa da seguinte forma: No primeiro mês daria um aumento de 5% e no segundo mês mais um aumento de 10%, pagando efetivamente (desembolsando) somente no segundo mês, ou seja, os aumentos se acumulariam para pagamento somente ao final.

— É muito fácil aplicar esse aumento sucessivo, basta aplicar 15% de aumento sobre o valor inicial. — diria você. Calma que a coisa não é tão fácil assim. Lembre-se da regra de ouro: você nunca sai ganhando. Os aumentos sucessivos serão sempre maiores que a soma algébrica das porcentagens.

Vamos desenvolver nosso exemplo:

Aumentamos 5% ao valor inicial, no caso, 300. Fica assim: 300 x 1,05 = 315.

Agora aplicaremos mais um aumento de 10%. Calculando, temos: 315 x 1,10 = 346,5.

Com isso quando tenho 300 reais e aplico um aumento de 5% e depois mais um aumento de 10%, terei que pagar ao final um valor de 346,50.

Veja que o aumento percentual real foi de 15,5% e não de apenas 15%. — Então como você sabe que o aumento real foi de 15,5%? — você pergunta. Respondo sua pergunta. Dividimos 346,5 por 300, ou seja, 346,50/300 = 1,155 (agora basta subtrair 1 ao resultado. Mas, porque 1? Simples. 1 equivale a 100%). 1,155 – 1 = 0,155 ou 15,5%.

Há outra forma de fazer aumentos sucessivos:

Quanto é um aumento de 5%. Sabemos que é 1,05

Quanto é um aumento de 10%. Sabemos que é 1,10

Multiplicamos os dois: 1,05 x 1,10 = 1,155

Por fim multiplicamos pelo valor inicial: 300 x 1,155 = 346,50

Perceba que o aumento aparente seria de 15%, entretanto o aumento real foi de 15,5%. Os aumentos sempre serão maiores do que parecem.

Descontos sucessivos

Vale a mesma regra utilizada nos aumentos sucessivos: você nunca ganha.

Exemplo: aplicar um desconto de 15% e depois mais um desconto de 10% sobre 300 reais.

Aplicando o primeiro desconto, temos: 300 x (100% – 15%) = 300 x 85% = 300 x 0,85 = 255.

Depois aplicamos mais um desconto de 10%. 255 x (100% – 10%) = 255 x 90% = 255 x 0,9 = 229,50.

— Não estou entendo o cálculo que você fez — você pensa. Creio que você não leu o método avançado de cálculo de aumento. Vá ao tópico correspondente e aprenda!

Vamos dividir 229,50 por 300. Então, 229,5/300 = 0,765. Subtraindo de 1, temos: 1 – 0,765 = 0,235 que significa 23,5%. Veja que aparentemente o desconto seria de 25% (15% + 10%), entretanto o desconto real foi de 23,5%

Nunca mais esqueça. Os aumentos sempre serão maiores que a soma algébrica, e os descontos sempre menores.

Misturando aumentos e descontos

Vamos aplicar um aumento de 30% e depois desconto de 10%, depois desconto de 20% sobre o valor de 250 reais. Algumas pessoas pensariam erroneamente que basta fazer cálculo (30% – 10% – 20%) = 0%. Não! Nunca faça isso! Isso é tão comum que quando esse assunto é abordado em alguma questão, as bancas trazem como resposta na alternativa A o valor da soma algébrica das porcentagens. Logicamente muitos alunos erram essa questão. Então vamos ver a forma eficiente de calcular de forma correta esse tipo de questão.

Primeiro passo: aumento de 30%, temos: 100% + 30% = 130% = 1,3

Segundo passo: desconto de 10%, temos: 100% -10% = 90% = 0,9

Terceiro passo: desconto de 20%, temos: 100% – 20% = 80% = 0,8

Quarto passo: multiplicar todos esse valores: 1,3 x 0,9 x 0,8 = 0,936

Quinto passo: multiplicar 250 por 0,936 = 250 x 0,936 = 234

Esquematizando o processo: