Operadores lógicos: conectivo OU
Nesse artigo aprenderemos sobre o operador lógico OU, também chamado de disjunção inclusiva. Iremos aprender os seguintes assuntos:
- Conceito de conectivo
- Disjunção (conectivo OU)
- Como entender a disjunção inclusiva
- Exemplos de disjunção inclusiva
- Tabela verdade da disjunção
- Diagrama lógico da disjunção inclusiva.
Conceito de conectivo
Começaremos com o conceito de conectivo. Conectivo é uma estrutura que liga duas ou mais proposições lógicas, dando a elas um determinado sentido (que pode ser de inclusão, exclusão, condicional, etc.)
Disjunção inclusiva
Mas o que é uma disjunção inclusiva? A disjunção inclusiva, também conhecida como conetivo lógico OU, traz a ideia de inclusão. Vejamos a seguinte sentença que possui uma disjunção inclusiva: “Vou à praia ou à festa”. Perceba que essa pessoa pode ir à praia, pode ir à festa, como também pode ir tanto à praia quanto à festa. Nessa situação essa pessoa não exclui nenhuma possibilidade de se divertir. E é por isso que a disjunção é chama de disjunção inclusiva, visto que ela não exclui as possibilidades dispostas. Ou seja, a pessoa que disse a frase estará falando a verdade quando for à praia, quando for à festa, ou também quando for à praia e à festa na mesma situação. Só há uma maneira de essa pessoa mentir ao falar “Vou à praia e à festa”: quando ela não for nem à praia e nem à festa.
Como entender a disjunção inclusiva
Nesse momento você pode se perguntar: como posso entender a disjunção inclusiva? Calma! Não se desespere. Depois dessa aula, você nunca mais esquecerá o mecanismo da disjunção.
Eis uma história para ilustrar a situação.
Em uma certa família brasileira, a mãe pede a um dos filhos que vá comprar café ou chá para fazer o café da manhã. O rapaz prontamente foi ao comércio e pediu ao atendente se havia para café para vender, pois havia esquecido qual era o outro item a ser comprado. Chegando à casa com o café em mãos, o entregou a mãe. Nessa situação será que o filho realmente atendeu ao pedido de sua mãe? A resposta é sim! Há outras situações em que o pedido da mãe seria tendido: se o rapaz comprasse apenas chá ou se o rapaz comprasse café e chá juntos. Só haveria uma situação em que o pedido da mãe não seria atendido: se o rapaz não comprasse nem café e nem chá. Podemos extrair dessa história que a disjunção inclusiva só será falsa quando as proposições que a compõem forem também falsas. Nos outros arranjos a disjunção sempre será verdadeira.
Exemplos de disjunção inclusiva
Temos as seguintes proposições simples:
p: Camila é estudiosa
q: Vicente é esforçado
Então,
p v q: Camila é estudiosa ou Vicente é esforçado
Como montar a tabela-verdade da disjunção
Agora iremos aprender a montar a tabela verdade da disjunção inclusiva.
Antes de tudo iremos construir uma tabela que possua 3 colunas e 4 linhas (podemos acrescentar mais uma linha que seria o cabeçalho). Fica assim:
A linha em azul será utilizada para o cabeçalho, isto é, nela teremos a informação da proposição p na primeira coluna, q na segunda coluna e na última coluna o resultado da disjunção p v q. Essas letras (p, q) representam proposições simples quaisquer.
Na primeira coluna iremos preencher com V, V, F, F no sentido de cima para baixo. Já na segunda coluna iremos preencher com V, F, V, F. Em artigos posteriores iremos trazer os detalhes sobre a tabela-verdade, explicando o mecanismo de formação dela. Depois de todos esses passos, teremos:
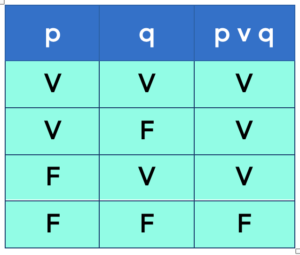
Creio que nesse momento irá surgir uma pergunta pertinente. Como descubro o resultado de p v q dá última coluna da tabela-verdade? Simples! Se você leu esse artigo desde o começo saberá que uma disjunção só será falsa quando as proposições que a compõem forem falsas, isto é, quando p e q forem falsas ao mesmo tempo. Nos outros arranjos sempre teremos como resultado um valor verdadeiro. E é por isso que somente o resultado da última linha é falso e os demais são todos verdadeiros. Simples, né.
Diagrama lógico da disjunção inclusiva.
Na figura abaixo temos o diagrama lógico da disjunção inclusiva.
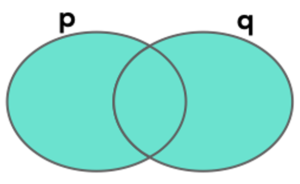
Disso podemos entender que a disjunção inclusiva é formada pelo conjunto p, mais o conjunto q, mais a interseção dos conjunto p e q.
Essa era a aula de hoje, bons estudos e até a próxima aula.