Nunca mais sofra com o se… então…
Nesse artigo iremos abordar um assunto que causa bastante confusão na cabeça dos alunos e é de longe o assunto mais cobrado quando se fala em operadores lógicos. Entretanto a partir de então a condicional não será um bicho de sete cabeças para você. Acredita nisso? Então vamos aos trabalhos. Que os jogos comecem!!!
Os assuntos a serem tratados aqui serão:
- O que é a condicional
- Como entender a condicional
- Exemplos de condicional
- Tabela verdade da condicional
- Diagrama lógico da condicional
- Como a condicional é cobrada em prova.
O que é a condicional
A condicional é o conectivo lógico que estabelece uma relação de suficiência e necessidade, nessa ordem, em relação a duas proposições lógicas (calma, você entenderá essa relação mais a frente, por enquanto apenas aceite isso). A forma de expressar uma condicional é se p, então q ou p → q. O símbolo que representa uma condicional é uma seta apontada na direção direita (→).
Como entender a condicional
Ah! Condicional, condicional, temida por todos os estudantes de lógica matemática, odiada por sua forma de ser. Basta! Basta! A partir de agora esse sentimento será extirpado de sua mente, não mais existirá. Sabe o porquê? Simples. Você realmente entenderá o que é uma condicional, ela não será um peso em sua vida, você a dominará de forma excelente. Talvez você esteja em dúvida quanto ao que eu estou falando, mas falo sério. Isso não é nenhuma brincadeira de mal gosto. Ao terminar essa aula você terá conhecimento suficiente para encarar as questões que envolvem a condicional com boa desenvoltura.
Vamos analisar a seguinte frase: Se José é cearense, então ele é brasileiro.
Temos duas proposições simples ligadas pelo conectivo se…então.
Vamos elencar algumas possibilidades sobre essas proposições, por meio de perguntas.
Primeira pergunta: se José é cearense, também ele será brasileiro? Verdade!
Segunda pergunta: se José é cearense ele não será brasileiro? Falso! Pois todo cearense é brasileiro, assim como todo paulista, maranhense, mineiro, etc…
Terceira pergunta: se José não for cearense, ele poderá ser brasileiro? Verdade! Visto que ele poderá ser mineiro, maranhense, paulista.
Quarta pergunta: Se José não for cearense, ele não poderá ser brasileiro? Verdade! Ele simplesmente pode ser de outra nacionalidade, assim não sendo nem cearense e nem brasileiro.
Se você leu atentamente as perguntas realizadas, percebeu que a segunda pergunta foi a única em que e resposta foi falsa. É por esse motivo que a condicional será falsa quando a primeira proposição for verdadeira e a segunda falsa, visto que ser cearense é verdadeiro, não ser cearense é falso e ser brasileiro é verdadeiro e não ser brasileiro é falso. Como assim, ainda não entendi. A proposição José é cearense é verdadeira, certo? Já a segunda proposição não será brasileiro é falsa, pois ser brasileiro é verdadeira. Pronto. Agora você nunca mais vai esquecer como funciona a condicional. Basta lembrar que todo cearense é brasileiro. Você pode trocar a a palavra cearense por paulista, ou maranhense, ou carioca, enfim, acho que você entendeu.
Exemplo de condicional
Vamos exemplificar uma condicional. Dadas duas proposições simples:
p: O carro está quebrado
q: Hoje não vamos passear
Formaremos a condicional assim:
p → q: Se o carro está quebrado, então hoje não vamos passear.
Nota: Há diversas outras formas de se formar uma condicional. Convém saber o formato delas também, pois caem bastante em prova.
Veja a tabela abaixo:
Expressões equivalentes a proposição se p, então q (p → q)
| Expressão | Exemplo |
|---|---|
| p somente se q | Estudo muito somente se passarei na prova |
| q, contanto p | Passarei na prova, contanto que tenha estudado muito. |
| no caso de p, q | No caso de estudar muito, passarei na prova. |
| se p, q | Se estudo muito, passarei na prova. |
| p implica q | Estudar muito implica que passarei na prova. |
| q, no caso de p | Passarei na prova, no caso de estudar muito. |
| q, pois p | Passarei na prova, pois estudo muito. |
| q, se p | Passarei na prova, se estudar muito. |
| p é suficiente para q | Estudar muito é suficiente para passar na prova. |
| q é necessário para p | Passar na prova é necessário para estudar muito. |
Nota: na tabela acima algumas expressões trocam as posições das proposições, fique atento a esse detalhe. Ora aparece p e depois q. Ora aparece q e depois p. Fique de olho.
Tabela verdade da condicional
Depois que entendemos como funciona a condicional, a criação da tabela-verdade desse conectivo lógico fica relativamente simples. Pela teoria sabemos que há apenas uma única forma de a condicional ter como resultado o valor de falso: quando a primeira proposição for verdadeira e a segunda for falsa. Pronto! Nos outros arranjos, sempre teremos resultado lógico da condicional como verdadeiro.
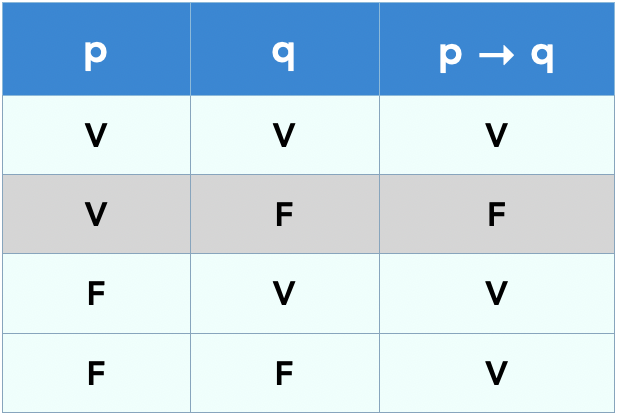
Diagrama lógico da condicional
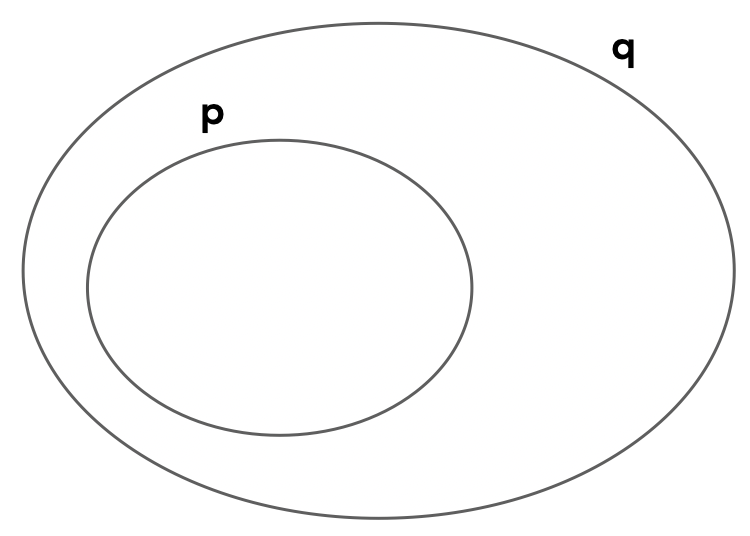
O diagrama lógico da condicional consiste no conjunto p contido no conjunto q. Assim posso transformar uma condicional em um diagrama lógico, em que a primeira proposição está inserida dentro da segunda proposição. Esquematizando podemos entender que a seta da condicional parte do centro para o exterior.
Como a condicional é cobrada em prova.
Eis essa questão da banca FUNDATEC que caiu em 2020.
O diagrama lógico que pode representar a proposição “Ser morador de Imbé é ser morador do Rio Grande do Sul” é mostrado na alternativa:
A)
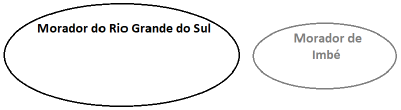
B)
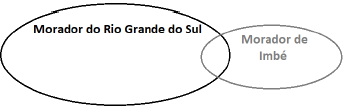
C)
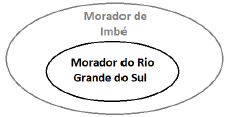
D)
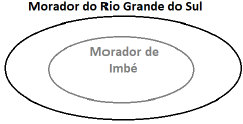
E)
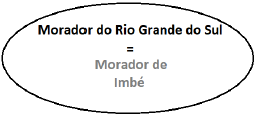
Analisando a frase: “Ser morador de Imbé é ser morador do Rio Grande do Sul”, podemos traduzi-la como “Todo morador de Imbé é morador do Rio grande do sul”. E isso significa que o conjunto dos moradores de Imbé está contido, isto é, dentro do conjunto das pessoas que moram no Rio grande do sul. A letra D corresponde perfeitamente ao que acabamos de explicar. Portanto a correta é a letra D.
Então até a próxima aula. Bons estudos!