Operadores lógicos: conjunção
Vamos abordar os seguintes assuntos:
- O que é a conjunção
- Como entender a conjunção
- Exemplo de conjunção
- Tabela verdade da conjunção
- Diagrama lógico da conjunção
- Como a conjunção é cobrada em prova.
O que é a conjunção
A conjunção é o conectivo lógico que liga proposições cujo resultado da operação equivale a uma interseção de conjuntos. O símbolo que indica uma conjunção é ( ∧ ) ou a letra ( e ).
Como entender a conjunção
Uma mãe tem dois filhos. Certa vez os dois estavam bagunçando a casa. Ela chegou para o mais velho e disse: Carlos, quero falar contigo e com o Bruno. Então o Carlos se apresentou para a mãe. Nesse momento você imagina que a mãe irá dar uma bronca nele. Não! Ela perguntou: cadê teu irmão? Eu quero falar com vocês dois.
Perceba que ela queria falar com o Carlos e o Bruno ao mesmo tempo. Ela não queria falar apenas com um dos dois. Dessa forma se comparecesse apenas Carlos ela iria reclamar, pois seu pedido não seria atendido. Também se aparecesse apenas Bruno, ela iria reclamar, pois não era o que ela queria. E se não aparecesse nenhum dos dois, aí ela virava uma arara, visto que todos a estavam ignorando. Então a única forma de obedecer ao pedido da mãe era que Carlos e Bruno comparecessem ao mesmo tempo para falar com ela. Assim funciona o conectivo “e” (a conjunção). A proposição composta p e q só é verdadeira quando os valores lógicos de p e q forem verdadeiros, do contrário será falso.
Exemplo de conjunção
Temos as seguintes proposições:
p: O ser humano é inteligente
q: A girafa é um animal exótico.
Então a conjunção dessas duas proposições é:
p ∧ q: O ser humano é inteligente e a girafa é um animal exótico.
Mas atenção! Há outras formas de indicar uma conjunção. Veja a seguinte conjunção:
p ∧ q: Marte é bela e Paulo é sorridente.
Essa frase poderia vir das seguintes formas:
p ∧ q: Marte é bela, mas Paulo é sorridente
p ∧ q: Tanto Marta é bela como Paulo é sorridente.
Portanto, fique atento a essas formas de indicar uma conjunção.
Tabela-verdade da conjunção
Para construirmos a tabela-verdade da conjunção vamos preencher a primeira coluna (cujo cabeçalho é p) com V, V, F, F. Na segunda coluna vamos preencher com V, F, V, F. A direção do preenchimento é de cima para baixo. Pois bem, como já sabemos que a conjunção só será verdadeira quando as proposições forem verdadeiras, fica fácil. Localizamos a linha horizontal em que tenha V e V. Nessa linha o resultado será verdadeiro ( V ). Nas demais linhas o resultado da conjunção será sempre falso ( F ).
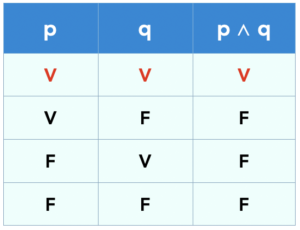
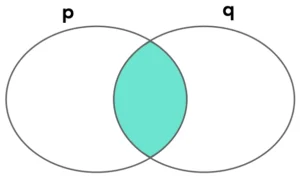
Diagrama lógico da conjunção
O diagrama lógico da conjunção é a interseção das proposições p e q. O conjunto não será formado apenas por p, ou apenas por q. Será formado por p e q ao mesmo tempo, ou seja, a interseção dos dois conjuntos. Veja na figura abaixo.
Como a conjunção é cobrada em prova.
Veja como a banca INSTITUTO MAIS cobrou esse assunto.
Assinale a alternativa que apresenta um exemplo de conjunção.
A) “Acordo cedo ou perco o emprego”.
B) “Sou mais velho que Olga e mais novo que Otávio”.
C) “Se fizer sol, irei viajar”.
D) “Todo número natural é inteiro”.
Na letra A, estamos diante de uma disjunção inclusiva, então não é o item correto.
Na letra B, temos duas proposições unidas pelo conectivo “e” (conjunção). Portanto essa é a questão correta.
Na letra C, temos uma condicional.
E por fim na letra D, temos uma proposição simples.
Então confirmamos a letra B como a correta.