Frações
Conceito de fração
Fração é a divisão entre dois números. Podemos compreender a fração como a parte ou pedaço de alguma coisa. Ela é representada por dois números separados por uma barra, em que a parte de cima se chama numerador e a parte de baixo se chama denominador.

Exemplo:
Marta, Raquel e Vera compraram uma barra de chocolate. Elas decidem que vão dividir essa barra em partes iguais para cada uma. Qual a fração que cada uma ficará?
Veja que temos 3 pessoas, logo a barra de chocolate será dividida por 3. Quando a barra de chocolate estiver quebrada em 3 pedaços cada uma das meninas pegará o seu pedaço.
Agora vamos montar a fração fazendo as seguintes perguntas:
Em quantas partes foi dividida a barra de chocolate?
Foi dividida por 3.
Com quantos pedaços cada menina ficou?
Cada uma ficou com 1 pedaço.
Podemos representar graficamente a situação.
Por isso, temos:
Frações próprias
São frações em que o numerador é menor do que o denominador. O resultado dessa fração será menor do que o inteiro.
Exemplo:
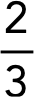
Frações impróprias
São frações em que o numerador é maior do que o denominador. O resultado desse tipo de fração será maior do que o inteiro.
Exemplo:
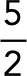
Frações mistas
São frações formadas por uma parte inteira e outra não inteira.
Exemplo:
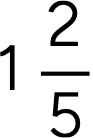
As frações mistas podem ser transformadas em frações normais, bastando apenas multiplicar o denominador pelo número da frente e depois somar com o numerador.
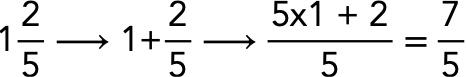
Perceba que multiplicamos o 5 (denominador) por 1 (número da frente) e depois somamos com 2 (numerador).
Frações equivalentes
São frações que mesmo que diferentes, representam a mesma quantidade de algo.
Exemplo:
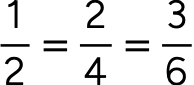
Ao multiplicar um número natural pelo numerador e pelo denominador podemos formar novas frações equivalentes a àquela.
Operação com frações
Somar e subtrair
Com denominadores iguais:
Quando os denominadores são iguais, soma-se os numeradores e mantém o denominador.
Exemplo:
Com denominadores diferentes:
Quando os denominadores são diferentes, deve-se fazer com que os denominadores fiquem iguais. Ou seja, devemos reduzir as frações ao mesmo denominador comum. Dessa forma podemos manter o denominador comum e somar os numeradores (veja regra anterior).
Exemplo:
Somar as frações abaixo
Primeiro passo: tirar o mmc entre os denominadores.

Nota: Se o maior denominador for múltiplo dos demais, este será o mmc. Veja que o 6 é múltiplo de 2 e de 3, por isso ele será o denominador comum.
Segundo passo: colocar o mmc no denominador de todas as frações, conforme o esquema abaixo.

Agora para se calcular os numeradores, pega-se o mmc e divide pelo denominador de cada fração e multiplica-se pelo numerador da respectiva fração.
Por fim, temos: (repete o denominador e soma-se os numeradores)
Nota 1: 15/6 pode ser simplificado dividindo ambos os números por 3, ficando 5/2.
Nota 2: A subtração segue o mesmo procedimento. A soma e a subtração podem vir na mesma expressão, mas o procedimento não muda.
Nota 3: Para somar um número que não está em forma de fração com um número em forma de fração, basta multiplicar o denominador da fração pelo número inteiro e somar ao numerador da fração. Exemplo:
Como multiplicar frações
A multiplicação de frações é realizada multiplicando numerador com numerador e denominador com denominador.
Exemplo: Multiplicar as frações abaixo
Nota 1: A fração 12/36 pode ser simplificada dividindo-se o numerador e o denominador por 12. Assim, 12/36 = 1/3. Essa última fração é chama de irredutível, pois não se pode simplificar além disso.
Nota 2: Acostume-se a fazer cancelamentos de números ao realizar multiplicações e divisões. Dessa forma você economizará muito tempo na resolução do cálculo.
Exemplo: simplificar a fração

Como dividir frações
A divisão de frações é realizada mantendo-se a primeira fração e multiplicando pelo inverso da segunda.
Exemplo: dividir as frações abaixo.
Veja que conservamos a primeira fração e multiplicamos pelo inverso da segunda.