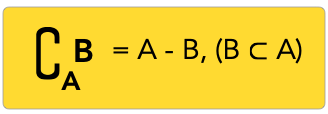Teoria dos Conjuntos

Conjunto é um agrupamento de qualquer coisa que tenha determinada característica. Um conjunto é representado por letra maiúscula do alfabeto.

Exemplos:

• Conjuntos das três primeiras letras do alfabeto.

A = { a, b, c }

• Conjuntos dos números naturais maiores que 10.

A = { 11, 12, 13… }

Nota: as reticências no final indicam que o conjunto é infinito.

• Conjunto dos dias da semana.

A = { segunda, terça, quarta, quinta, sexta, sábado, domingo }

Representação de um conjunto

• Por enumeração: 

A = { 3, 4, 5 }

• Por diagrama

• Por linguagem simbólica: 

A = {x | x maior que 5}. Lê-se dessa forma: o conjunto A é igual a x tal que x é maior que cinco.

Conjunto vazio

Não possui elementos. É representado pelos símbolos Ø ou  { }

Exemplo: conjunto dos meses do ano que possuem 32 dias.

A = Ø

Veja que há meses do ano com 32 dias, por isso esse conjunto é vazio

Nota: O símbolo { Ø } não representa um conjunto vazio. Na verdade, significa um conjunto unitário. Cuidado, pois as bancas de concursos utilizam essa pegadinha.

Conjunto unitário

Possui apenas um elemento.

Exemplo: conjunto dos números naturais compreendidos entre 4 e 6.

A = { 5 }

Conjunto finito

Possui número conhecido de elementos

Exemplo: conjunto do dias da semana.

A = { segunda, terça, quarta, quinta, sexta, sábado, domingo }

Conjunto infinito

Conjunto em que não conhecemos a quantidade de elementos.

Exemplo: conjunto dos números pares.

Subconjunto

Quando um conjunto A está contido no conjunto B dizemos que o conjunto A é subconjunto de B, ou seja, todo elemento de A é também elemento de B.

Representamos assim: A ⊂ B

Nota: Existem outras formas de nomenclaturas para representar o símbolo está contido (⊂).

• A está contido em B
• A é subconjunto de B
• A é parte de B

Conjunto das partes

Formado por todos os subconjuntos de A. É representado por P(A).

Exemplo: conjunto das partes do conjunto A = {1, 2}

P(A) = { Ø, {1}, {2}, {1,2}}

Nota: o número de subconjuntos (conjunto das partes) pode ser calculado  pela fórmula 2ⁿ, em que o “n” é o número de elementos do conjunto.

No exemplo o conjunto A possui 2 elementos, portanto o conjunto das partes desse conjunto é 2ⁿ = 2² = 4. Então o conjunto das partes do conjunto A possui 4 elementos.

Relação de pertinência e inclusão

Quando relacionamos um conjunto com seus elementos estamos utilizando a relação de pertinência. Por outro lado, quando relacionamos conjunto com conjunto estamos utilizando a relação de inclusão.

Propriedades da inclusão

Primeira propriedade: o conjunto vazio está contido em qualquer conjunto.

Simbolizamos assim: Ø ⊂ A:

Segunda propriedade: qualquer conjunto está continho nele mesmo, ou seja, qualquer conjunto é subconjunto dele mesmo.

Simbolizamos assim: A ⊂A.

Conjuntos iguais.

Dois conjuntos são iguais quando os elementos que pertencem a A, também pertençam a B e quando os elementos que pertencem a B também pertençam a A. Ou seja, quando possuem os mesmos elementos.

Exemplo:

A = {a,b,c}

B={c,b,a}

Nota: perceba que a disposição dos elementos não é levado em consideração.

Exemplo:

C={1,2}

D={1,2,2,2}

Nota: embora haja elementos que se repetem, os conjuntos, pela definição, ainda são iguais.

Operações de conjuntos

Temos as seguintes operações quando tratamos com conjuntos:

• União
• Interseção
• Diferença
• Complementar

União

A união entre dois conjuntos A e B se dá pelos elementos que pertencem a A ou pelos elementos que pertencem a B. Representamos assim: A ⋃ B

A ⋃ B = { x | x ∈ A ou x ∈ B }. Lê-se: A união B é igual a x, tal que x pertence ao conjunto A ou x pertence ao conjunto B.

Exemplo:

A = { a, b, c }

B = { c, d }

A U B = { a, b, c, d }

Representação da união pelo diagrama de Venn

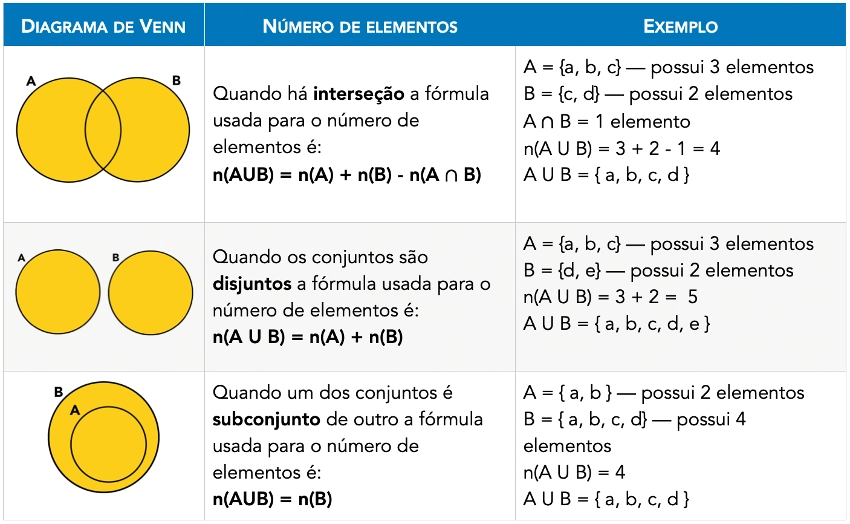
Propriedades de união

• A união entre dois conjuntos iguais é igual ao próprio conjunto. 

Exemplo: A ⋃ A = A

• O conjunto vazio é o elemento neutro da união

A ⋃ Ø  = A

• Propriedade comutativa.

Mudando-se a posição dos conjuntos o resultado não se altera. Ou seja, A união B é o mesmo que B união A.

A ⋃ B = B ⋃ A

• propriedade associativa

Fazer associações entre os conjuntos não altera os resultado.

(A ⋃ B) ⋃ C = A ⋃ (B ⋃ C)

Interseção

A interseção entre dois conjuntos A e B é dado pelos elementos em comum aos dois conjuntos, ou seja, correspondem aos elementos que pertencem a A e a B.

A ⋂ B = { x | x ∈ A e x ∈ B }. Lê-se: A interseção antre A e B é igual a x, tal que x pertence a A e x pertence a B.

Exemplo:

A = {a,b,c}

B = {c,d}

 A ⋂B = {c}

Propriedades da interseção

• A interseção entre dois conjuntos iguais é o próprio conjunto.

Exemplo: A ⋂ A = A

• O conjunto universo é elemento neutro da interseção.

Exemplo: A ⋂U = A

• A mudança de posição não altera o resultado (propriedade comutativa)

A ⋂B = B ⋂ A

• O rearranjo dos conjuntos não altera o resultado (propriedade associativa)

Exemplo: (A ⋂ B) ⋂ C = A ⋂(B ⋂C)

Representação da interseção pelo diagrama de Venn

Nota: a fórmula utilizada é a mesma de união só que com um arranjo diferente.

Diferença de conjuntos.

Dados dois conjuntos A e B, a diferença de A menos B é dada pelos elementos que pertencem a A e não pertencem a B.

A – B = { x | x ∈ A e x ∉B }. Lê-se A menos B é igual a x, tal que x pertence a A e x não pertence a B.

Exemplo:

A = { 1, 2, 3, 3 }

B = { 2, 4, 5 }

A – B = { 1, 3 }

B – A = { 5 }

Representação da diferença pelo diagrama de Venn

Conjunto Complementar

Vou falar algo que talvez você nunca ouviu sobre o complementar de um conjunto. O complementar é um formato de de conjunto que lembra a forma de um anel. — Como assim a forma de um anel? você pergunta. — Eu pensava que o complementar de um conjunto era preciso subtrair os dois conjuntos, quando um está contido no outro. 

Sim, você está certo. Mas você não irá precisar decorar todo esse processo para aplicar o complementar, a menos que você queira. A partir de então vou explicar o complementar de um conjunto e depois vou ensinar uma forma bastante eficiente de nunca mais esquecer esse assunto.

Existem algumas condições para o complementar de um conjunto.

• Primeira condição: deve haver a diferença entre dois conjuntos, ou seja, A – B.
• Segunda condição: o conjunto B deve estar contido no conjunto A.

Em termos matemáticos denomina-se o complementar de B em relação a A por:

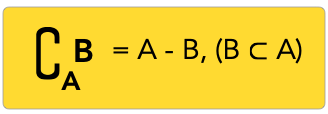
O diagrama abaixo mostra a forma do complementar de B em relação a A.

Agora a forma de nunca mais esquecer como é dado o complementar de um conjunto, basta lembrar que o diagrama do complementar forma um anel. Lembre-se do anel! — Tudo bem que o diagrama parece um anel, mas como posso a partir do diagrama retornar a fórmula do complementar? — você questiona. 

Simples! Devemos representar a parte amarela do diagrama. Veja que para fazermos isso devemos subtrair o conjunto maior do menor, ou seja, A – B. Outro detalhe que podemos perceber é que o conjunto B está contido no conjunto A. — Acho que entendi, mas como sei se é o complementar de A em relação a B ou B em relação a A? — você indaga. Boa pergunta. O nome é “complementar” de um conjunto, ou seja, aquilo que precisa ser completado. Então, só posso complementar alguma coisa que seja menor que outra. Assim o complementar será sempre o conjunto menor, isto é, o conjunto que está contido no outro. Simples, não? E é por isso que representamos o complementar de B em relação a A por: